Give Feedback What do you think of standard deviation calculator?
Worst
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
Standard deviation calculator finds the standard deviation of sample and population data. This tool also provides variance of sample and population data, mean, differences, the sum of differences, and the square of differences.
In statistics, standard deviation measures the spread of data distribution. It measures the typical distance between each data point and the mean. In other words, it shows how the data spread around the mean or average.
Standard deviation is the square root of the variance. It is denoted by s for sample data and sigma (σ) for population data.
The formula for sample standard deviation is:
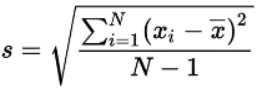
The formula for population standard deviation is:
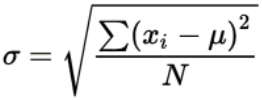
Below are a few examples of standard deviation solved by our mean and standard deviation calculator.
Example 1: For sample data
Find the standard deviation of the given sample data,
1, 5, 12, 18, 24
Solution:
Step 1: Take the given information and find the mean of the sample data.
Sample data = 1, 5, 12, 18, 24
Total observation = N = 5
Mean of sample data = Σxi/N = (1 + 5 + 12 + 18 + 24)/5
Mean of sample data = x̅ = 60/5 = 12
Step 2: Find the difference and square of the difference of each data value.
| xi | (xi - x̅) | (xi - x̅)2 |
| 1 | (1 - 12) = -11 | (-11)2 = 121 |
| 5 | (5 - 12) = -7 | (-7)2 = 49 |
| 12 | (12 - 12) = 0 | (0)2 = 0 |
| 18 | (18 - 12) = 6 | (6)2 = 36 |
| 24 | (24 - 12) = 12 | (12)2 = 144 |
| Σ(xi - x̅)2 = 350 |
Step 3: Substitute the calculated terms in the formula of sample standard deviation.
s = √(350/(5-1))
s = √(350/4)
s = √(87.5)
s = 9.3541
Example 2: For population data
Find the standard deviation of the given population data,
11, 24, 26, 31, 36, 40
Solution:
Step 1: Take the given information and find the mean of the sample data.
Population data = 11, 24, 26, 31, 36, 40
Total observation = N = 6
Mean of population data = Σxi/N = (11 + 24 + 26 + 31 + 36 + 40)/5
Mean of population data = µ = 168/6 = 28
Step 2: Find the difference and square of the difference of each data value.
| xi | (xi - µ) | (xi - µ)2 |
| 11 | (11 - 28) = -17 | (-17)2 = 289 |
| 24 | (24 - 28) = -4 | (-4)2 = 16 |
| 26 | (26 - 28) = -2 | (-2)2 = 4 |
| 31 | (31 - 28) = 3 | (3)2 = 9 |
| 36 | (36 - 28) = 8 | (8)2 = 64 |
| 40 | (40 - 28) = 12 | (12)2 = 144 |
| Σ(xi - µ)2 = 526 |
Step 3: Substitute the calculated terms in the formula of sample standard deviation.
σ = √(526/6)
σ = √(87.6667)
σ = 9.363
Khan Academy. (n.d.). What is the standard deviation? | Khan Academy.
Criticalvaluecalculator.com is a free online service for students, researchers, and statisticians to find the critical values of t and z for right-tailed, left tailed, and two-tailed probability.
