By following the below steps you can evaluate the probability of the given data:
Give Feedback What do you think of poisson distribution calculator?
Worst
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
The Poisson distribution calculator calculates the probability of the given data, it calculates all the possible probabilities according to the rules of the Poisson distribution. I.e., For Exactly, For Less than, For At most, For More than, For At least.
In the probability theory, the Poisson distribution is used to calculate the discrete probability, as a result, it gives the probability of an event occurring multiple times (x).
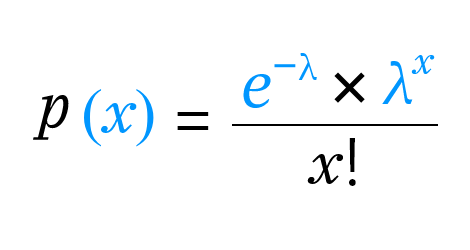
Just like the other discrete probability distributions, the Poisson distribution also has some properties that are as follows:
The mean of the Poisson distribution is given by lambda (λ).
The standard deviation of the Poisson distribution is the square root of the mean given by √(λ).
This section explains the method of evaluating probability using the Poisson distribution.
Example 1:
Calculate all the possible probabilities if the average rate of occurrence is 5 and the Poisson random variable is 1.
Solution:
Step 1: Extract the data.
Average rate of occurrence = λ = 5
Poisson random variable = x = 1
Euler’s constant = e = 2.718
Step 2: Calculation
For exactly P (x = 1):
Formula:
P(x) = (e−λ × λx) / x!
Values:
e = 2.718
x = 1
λ = 5
For Probability: P(x = 1)
P(1) = {(2.718) −(5) × (5)1} / 1!
P(1) = 0.00674 × 5
P(x = 1) = 0.03371
For Probability: P(x < 1)
P(0) = {(2.718) −(5) × (5)0} / 0!
P(0) = 0.00674
P(x < 2) = P (0)
P(x<1) = 0.00674
For Probability: P(x ≤ 1)
P(0) = {(2.718)−(5) × (5)0} / 0!
P(0) = 0.00674
P(1) = {(2.718)−(5)×(5)1} / 1!
P(1) = 0.03371
P(x ≤ 2) = P(0) +P(1)
P(x≤1) = 0.04045
For Probability: P(x>1)
P(x > 2) = 1 - P(x ≤ 2)
P(x>1) = 0.95955
For Probability: P(x≥1)
P(x ≥ 2) = 1 - P(x < 2)
P(x≥1) = 0.99326
Poisson Distribution - an overview | ScienceDirect Topics
This report is generated by criticalvaluecalculator.com
Criticalvaluecalculator.com is a free online service for students, researchers, and statisticians to find the critical values of t and z for right-tailed, left tailed, and two-tailed probability.
