Linear Regression

Linear regression calculator:

The Linear regression calculator calculates the linear regression between two data sets, say X & Y. It also calculates the mean and covariance of both sets. It gives a step-by-step solution to the problems.

What is linear regression?

In statistics, linear regression is a linear approach for modeling the relationship between a scalar response and one or more dependent and independent variables. The case of one variable is called simple linear regression for more than one, the process is called multiple linear regression.

General formula: 

The general formula of linear regression is as follows:

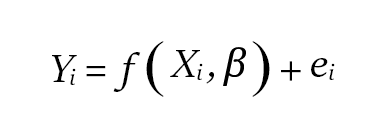
In the above formula:

• “Y_i” is the dependent variable
• “f” is the function
• “X_i” is the independent variable
• “β” is an unknown parameter
• “e_i” are the error term.

The equation of a line “y = mx + c” is also used to calculate the linear regression.

Method of calculating the linear regression:

In the following example, the method to calculate the linear regression is explained briefly.

Example 1:

Calculate the linear regression of the following data sets

X = 5, 3, 8, 4, 2, 7

Y = 43, 6, 4, 55, 1, 9

Solution:

Step 1: Calculate the mean of the data sets.

Mean of X = (5 + 3 + 8 + 4 + 2 + 7) / 6

Mean of X = (29) / 6

Mean of X = 4.833

Mean of Y = (43 + 6 + 4 + 55 + 1 + 9) / 6

Mean of Y = (118) / 6

Mean of Y = 19.667

Step 2: Calculate slope m

Slope = ​m = {(6 × 550) − (29 × 118)} / {6 × 167 − 841}

Slope = ​m = −122 / 161

Slope = ​m = -0.7578

Step 3: Calculate y-intercept “c”

y-intercept = c = {(118) − (−0.7578 × 29)} / 6

y-intercept = c = 23.3294

​Step 4: Put the values in the straight-line equation to find out the regression equation

y = mx + b

y = −0.7578x + 23.3294

References

Linear regression | Wikipedia.

What is linear regression? | Linear regression.