Hypothesis Testing Calculator

Hypothesis testing calculator is a statistical tool used to perform hypothesis testing for t-values and p-values to reject or select hypotheses (H₀ or H₁). Our hypothesis test calculator conducts the tests for the selection of raw data, z-value, and mean, standard deviation, & sample size.

This hypothesis calculator provides detailed step-by-step calculations that help to understand the process of rejecting or failing to reject the null hypothesis. It also gives a download feature that allows users to download the results in PDF files.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to test the assumptions for a given data and parameters. It is a systematic procedure to decide whether the results of a research analysis or study support a particular theory that applies to population data. 

This process formulates two hypotheses: 

• Null hypothesis (H₀), represents a statement of no effect or difference. 
• Alternative hypothesis (H₁) indicates the presence of an effect or difference. 

In testing use the sample/population/raw data and perform the t-test & p-test. Then draw the results to reject or fail to reject the null hypothesis by comparing the critical value (P, T, & Z) results.

Types of Hypothesis Testing

The basic types of hypothesis testing are based on the direction such as one-tailed tests (right-tailed and left-tailed) and two-tailed tests. Hypothesis testing is further categorized by the type of test (T-test, P-test, chi-square test, & Z-test) that is performed for hypothesis testing according to the nature of the data. 

Directional Hypothesis Testing

Directional hypothesis testing is used to determine the relationship between variables or population parameters in a specific direction. In this testing find the values by using tests like t-test, z-test, and p-test to locate the rejection region on the distribution curve along left, right, and two-tailed.

• One Tail: This test is used when to predict the directional prediction of the data values along one side of the curve. Also, determine the significant relation between the calculated & critical values.

1. Right-tailed: The right tail is used to reject or select a null hypothesis if the population parameter is greater than the critical value. Right tail is also known as the upper tail.
   
2. Left-tailed: The left tail also known as the lower tail test that used to reject or select a hypothesis. It is used for testing if the population parameter is less than the critical value.

• Two Tail: This test is used if the population parameter is different from the critical value to select or reject the H₀. In this critical region lies on both sides of the distribution curve and two tails are also known as a non-directional hypothesis testing method.

Hypothesis Testing with T-Test

T-test testing is used to compare the means of two groups. T-test hypothesis testing is performed on the data when the sample size is small and the population SD value is unknown. 

• If “T_calculated ≤ T_critical”: Reject null hypothesis.
• If “T_calculated ≥ T_critical”: Fail to reject null hypothesis.

Hypothesis Testing with Z-Test

Z Test hypothesis testing can also be used to compare the mean of two samples/population data sets. Z-hypothesis testing is similar to T-test testing but it is used for greater or equal to 30 sample size. It is performed when the population standard deviation is known or the sample size is large. 

• If the Z ≤ Z_α: Reject null hypothesis.
• If the Z ≥ Z_α: Fail to reject null hypothesis.

Hypothesis Testing by P-Value

P hypothesis test is used to decide whether to reject or fail to reject the null hypothesis. In p-testing find the p-value by using the significance level and degrees of freedom of the data set.

• If the p-value ≤ α: Reject the null hypothesis.
• If the p-value ≥ α: Fail to reject reject the null hypothesis.

Hypothesis Testing by Chi-square

Chi-square is another hypothesis-testing method that is used to determine the significant association between two categorical variables. It tests the independence of two categorical variables by comparing observed and expected frequencies. If the observed data differs significantly from the expected data then categories have a significant relation. 

• If the χ²_calculated ≤ χ²_critical: Reject the null hypothesis.
• If the χ²_calculated ≥ χ²_critical: Fail to reject the null hypothesis.

Hypothesis Testing Formula

The hypothesis testing formula depends on the use of tests according to the type of data, sample size, and population distribution. Some common hypothesis testing formulas for respective tests are given below:

T-test Formula

T-formula is used in the t-test hypothesis testing when the sample size is less than 30 and the sample/population standard deviation is unknown.

T = (x̄ - μ)/(s/√n)

Where:

• x̄: Sample mean
• μ: Population mean
•  s: Sample standard deviation
• n: Sample size

Z-test Formula

Z-formula is used in the z-test hypothesis testing when the sample size is greater than 30 and the sample/population standard deviation is known. 

Z = (x̄ - μ)/(σ/√n)

Where:

• x̄: Sample mean
• μ: Population mean
• σ: Population standard deviation
• n: Sample size

Chi-Square Formula

Chi-square formula is used in the chi-square testing for the nonparametric and normal distribution data by using the observed & expected frequency.

χ² = Σ [(O - E) ² / E]

Where:

• Χ² : Chi-square value 
• O : Observed frequency
• E : Expected frequency

How to do Hypothesis Testing? 

To understand how to perform the hypothesis experiment, just follow the below hypothesis testing steps:  

• Formulate the null hypothesis (H₀) & alternative hypothesis (H₁) and specify the test is one-tailed (left or right) or two-tailed.
• Select the hypothesis test (Z-test, T-test) and significance level (α) to identify the corresponding critical region or threshold.
• Calculate the test statistic based on the sample data with the appropriate formula (e.g., z-score, t-score, or χ²).
• Now, calculate the critical value according to the significance level and degree of freedom for selected test by by using the distribution table. For quick critical value results try our critical value calculator.
• Compare the test statistic value with the critical value for respective conditions and p-value with the significance level (α) to conclude the results i.e., reject or select H₀. 

Hypothesis Testing Example

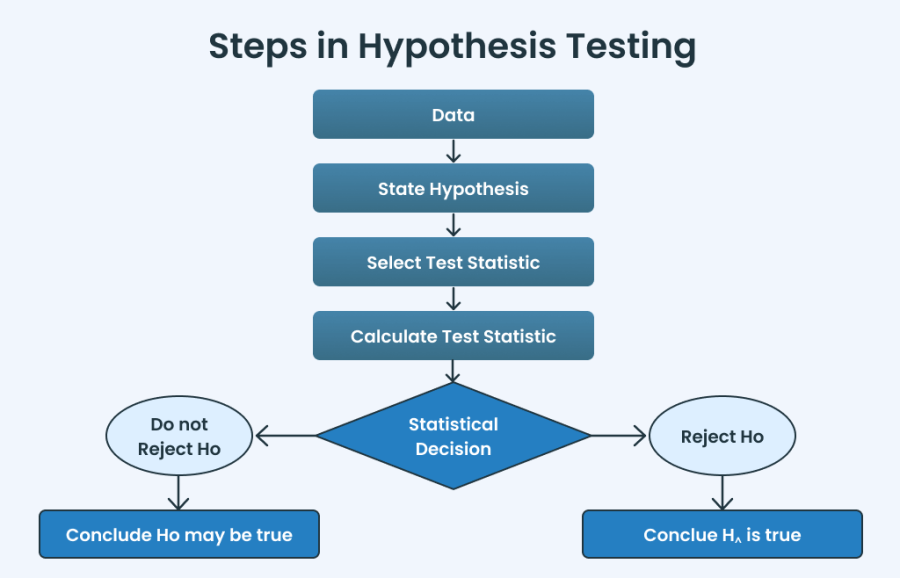
Here we perform the hypothesis testing for common applications with detailed steps to claims the hypothesis is true or not for the given raw data, or mean, proportions, and standard devaitions values. 

Example 1: A factory claims that the average weight of its product is 500g. A quality control officer takes a sample of 30 products and finds a sample mean of 495 grams with a standard deviation of 10 grams. Test at a 5% significance level whether the factory’s claim is true.

Solution:

In the given data, the sample size is 30, and the standard deviation is known. Thus, we will apply the z-hypothesis test for this analysis.

Step 1: Make the hypothesis. 

Null Hypothesis (H₀): The mean weight is 500 grams (μ=500).

Alternative Hypothesis (H₁): The mean weight is not 500 grams (μ≠500).

Step 2: Note the significance level and data.

α = 0.05, x̄ = 495, σ = 10, μ = 500, n = 30

Step 3: Now, calculate the test statistic value by using z-formula.

  z = (x̄ - μ) / (σ / √n)

  z = 495-500/(10/√30) = -2.74

Step 4: Now, find the critical value using the level of significance.

critical value for a two-tailed test = Z_critical= ±1.96

Step 5: Compare the test statistic value with the critical value to conclude the results.

Since, “-2.74” falls outside the range of the critical values, “if Z > Z_α then reject H₀​”.

Step 6: Now, Conclude the results.

There is sufficient evidence to reject the null hypothesis.

To verify the results, use our above hypothesis testing calculator. 

Frequently Asked Questions

What is the significance level in hypothesis testing?

In hypothesis testing, the “significance level” is a predefined probability that rejects a null hypothesis when the condition is true. It is denoted by the Greek symbol “α”.

What is the purpose of hypothesis testing?

Hypothesis testing is used to study results that support a theory or population. This statistical process uses sample data to assess hypothesis or claim population parameters based on sample data.

What is a type 1 error in hypothesis testing?

A type 1 error occurs in hypothesis testing when a researcher rejects a true null hypothesis and makes false results. This error is also known as a false positive.

Why is hypothesis testing important?

Hypothesis testing is essential because it provides a structured method to evaluate results whether data supports a particular claim or assumption for given data. 

What is the p Value in Hypothesis Testing?

The p value is used as a decision factor to determine if the hypothesis is significant or not. The null hypothesis can either be rejected or fail to reject by comparing the p-value and alpha level.